Ավելորդ է այն, ինչ կա. Հայեցակարգի իմաստը

2024 Հեղինակ: Henry Conors | [email protected]. Վերջին փոփոխված: 2024-02-12 08:45

Հոդվածում նկարագրվում է վիճակագրության դերը՝ որպես գիտություն։ Դիտարկված է կուրտոզի հայեցակարգը և դրա կիրառումը գիտության մեջ:

Վիճակագրություն. Հիմնական հայեցակարգ

Վիճակագրությունը մաթեմատիկական գիտության հիմնական ածանցյալն է: Այս առարկան պատկանում է մի շարք սոցիալական առարկաների, որոնք ուղղված են ուսանողների մոտ ձևավորելու աշխարհայացքի պատկերը և իրադարձությունների գրագետ վերլուծությունը:

Վիճակագրությունն ուսումնասիրում է մարդկանց կյանքում տեղի ունեցող բոլոր տեսակի գործընթացներն ու իրադարձությունները, ընդգծում նրանց օրինաչափությունները և ամեն ինչ ներկայացնում կարճ վիճակագրական հաշվետվությունների տեսքով։ Նման գիտությունը սոցիալապես օգտակար է և մշտական կատարելագործում է պահանջում։ Ավելորդ - ինչ է դա: Սա գրաֆիկական վիճակագրության հիմնական հասկացությունն է, որն օգնում է որոշել կատարյալ հաշվարկի ճիշտությունը: Կուրտոզը չպետք է ունենա ուժեղ շեղում։

Վիճակագրությունը թույլ է տալիս բավարարել մարդկանց որոշակի երևույթի, իրադարձության և այլնի վերաբերյալ վստահելի տեղեկատվության կարիքը: Որոշելով կյանքի գործոնների դինամիկան, դրանց անկումը, լճացումը կամ աճը, սա հենց այն է, ինչ անում է այս գիտությունը:

Ժամանակակից աշխարհում վիճակագրությունը գիտական ասպարեզում զբաղեցնում է գլխավոր տեղերից մեկը։ Դիտարկենք «կուրտոզ» հասկացությունը։ Ի՞նչ է վիճակագրական նպատակը և դիտարկումը: Որտե՞ղ են կիրառվում այս հասկացությունները: Այս ամենի մասին ավելին կարդացեք այստեղհոդված.

Ի՞նչ է քրտոզը վիճակագրության մեջ:

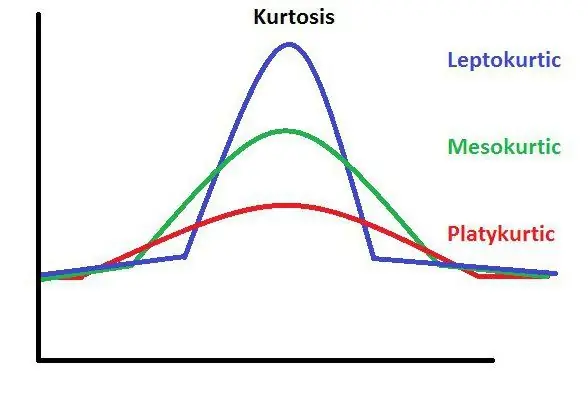
Կուրտոզը վիճակագրական հասկացություն է, որը ներկայացնում է յուրաքանչյուր գագաթի հստակությունը բաշխման գրաֆիկում: Դրա ճշգրիտ հաշվարկի համար կա հատուկ բանաձև։

Ակնկալությունը նշում է, որ վիճակագրական տվյալների ավելի հավասարաչափ բաշխման համար կուրտոզը պետք է հավասար լինի դրական թվի: Բառացիորեն այս հասկացությունը նշանակում է նորմայից որոշակի շեղում և վիճակագրական համակարգի հետագա աննորմալ զարգացում կամ գործարկում։

Վիճակագրական գծապատկերի վրա երկարատև արտահայտությունը կարող է ցույց տալ սխալ ուսումնասիրություն կամ սխալներ գրաֆիկի սկզբնական տվյալների մեջ: Նման հայեցակարգն իր բնույթով սկալյար է, ինչը նշանակում է, որ վերջնական հաշվարկի արդյունքում պետք է ստացվի մի թիվ, որը չի պարունակի փոփոխականներ կամ օժանդակ գործառույթներ: Ահա թե ինչ տեսք ունի կուրտոզը։

Ինչ է սիմետրիկ և ասիմետրիկ բաշխումը

Կուրտոզը, որը կապված է սիմետրիկ տեսակի բաշխման հետ, հավասար է զրոյի։ Սա կարելի է հստակ ցույց տալ գրաֆիկով: Ասիմետրիկ գրաֆիկը ցույց է տալիս մի թիվ, որը զրոյական չէ: Ահա թե ինչպես է նշանակվում կուրտոզը։

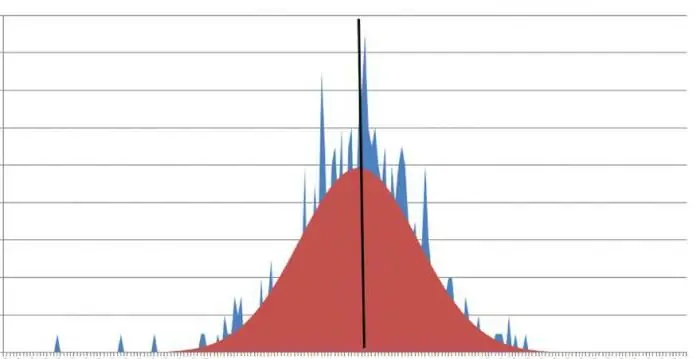
Ի՞նչ է գագաթի սրությունը: Գրաֆիկը, որն ունի սուր գագաթներ, ցույց է տալիս, որ կուրտոզի արժեքը զրոյից փոքր թիվ է: Հաճախ լինում են իրավիճակներ, երբ տվյալ հասկացությունը չի կարող արտահայտվել առանձին արժեքով։ Այս դեպքում այն մոտենում է մինուս կամ գումարած անսահմանությանը: